Question 1
Given that there are 715 rows in total, I have tried 8, 10, 12, 15 folds and the corresponding average of train and test scores are as the following:
- k = 8
- train score: 0.019477178686178
- test score: -0.024545646835335944
- k = 10
- train score: 0.019514638368914018
- test score: -0.037502267848572614
- k = 12
- train score: 0.019399126134301125
- test score: -0.025932644957946994
- k = 15
- train score: 0.019206809563629627
- test score: -0.036841997269859754
For all the above choices of folds, the scores are all pretty far from 1. For test scores those are even below zero. Those indicate that linear model fitted in this way is not able to produce reliable result.
Question 2
Same choices of number of folds is applied here, and the corresponding average of train and test scores are as the following:
- k = 8
- train score: 0.01947717868617793
- test score: -0.024545646835334625
- k = 10
- train score: 0.019514638368914004
- test score: -0.037502267848572315
- k = 12
- train score: 0.019399126134301115
- test score: -0.025932644957947327
- k = 15
- train score: 0.019206809563629655
- test score: -0.03684199726985993
All the training and testing scores are still extremely small or even negative. In fact, there is not much difference between the scenario with and without the standardizaiton of features. Standarzing features is not the way to improve the performance of model.
Question 3
Features not standardized
For each choice of fold, the alpha is chosen between a large enough range in order to find the one corresponding to the global maximum of average testing score:
- k = 8
- optimal alpha value: 523.232
- train score: 0.019
- test score: -0.023
- k = 10
- optimal alpha value: For this one I have tried a range of [0,8000]. The highest average testing score keep increasing as the alpha value increases. However, as the graph shows the curve is already pretty flat and increasing alpha may not be able to help with testing score much. Hence although I did not find the global maximum, I took 8000 as the approximate of optimal alpha value.
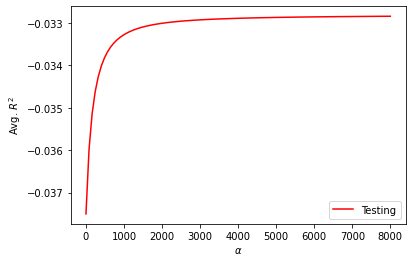
- train score: 0.018
-
test score: -0.033.
- k = 12
- optimal alpha value: 3232.323
- train score: 0.018
- test score: -0.022
- k = 15
- optimal alpha value: Similar with the k = 10 case, the global maximum of average testing score is not able to be found when alpha is chosen between [0,10000] but the increasement is already small enough to be ignored when alpha = 10000, so I took that as the approximate of optimal alpha value.
- train score: 0.017
- test score: -0.03
Features standardized
- k = 8
- optimal alpha value: 909.091
- train score: 0.017
- test score: -0.016
- k = 10
- optimal alpha value: 707.071
- train score: 0.017
- test score: -0.031
- k = 12
- optimal alpha value: 909.091
- train score: 0.017
- test score: -0.016
- k = 15
- optimal alpha value: 2222.22
- train score: 0.002
- test score: -0.053
Conclusion: Based on the training and testing scores above, the ridge regression still do not improve much about the performance of model no matter features are standardized or not. For each choice of number of folds, the testing score corresponding to the optimal alpha value is still above 0.
Question 4
Given that there are 659 observations in total for this dataset, the previous choice of k-fold (8, 10, 12, 15) is still sensible choice for this dataset.
Linear regression with out standardization of features
- k = 8
- train score: 0.004828895997905758
- test score: -0.05882744471588147
- k = 10
- train score: 0.004454887667329499
- test score: -0.061630609940973836
- k = 12
- train score: 0.0043661985278358835
- test score: -0.061090030222472336
- k = 15
- train score: 0.004109840416140501
- test score: -0.06028445451485857
Linear regression with standardization of features
- k = 8
- train score: 0.004828895997905799
- test score: -0.05882744471587825
- k = 10
- train score: 0.004454887667329444
- test score: -0.0616306099409739
- k = 12
- train score: 0.004366198527835828
- test score: -0.06109003022247352
- k = 15
- train score: 0.004109840416140501
- test score: -0.060284454514857845
For the ridge regression, although previous analysis of charleston_ask.csv suggests little difference betweem the performance of model with or without standardization of features. I still try both for ridge regression, since the above observation may not be able to applied to this different dataset.
Ridge regression without standardization of features
- k = 8
- approximate optimal alpha value (for the same reason as the above scernario): 10000
- train score: 0.002
- test score: -0.046
- k = 10
- approximate optimal alpha value: 10000
- train score: 0.002
- test score: -0.052
- k = 12
- approximate optimal alpha value: 10000
- train score: 0.002
- test score: -0.05
- k = 15
- approximate optimal alpha value: 10000
- train score: 0.002
- test score: -0.055
Ridge regression with standardization of features
- k = 8
- optimal alpha value: 3939.394
- train score: 0.001
- test score: -0.043
- k = 10
- optimal alpha value: 2525.253
- train score: 0.002
- test score: -0.005
- k = 12
- optimal alpha value: 9090.909
- train score: 0.001
- test score: -0.047
- k = 15
- optimal alpha value: 2222.22
- train score: 0.002
- test score: -0.053
Conclusion: For all the above types/specifications of models, the trainning score are still really small and the testing score are all above zero. This indicates that these fitting methods do not work well either for this different dataset.
Question 5
For this one I tried two additional choices for k (4,6) in order to see the trend more completely. The table on the above are results for charles_ask.csv and the table below are results for charles_act.csv. The highest training and testing score for each type of model are marked in blue and green respectively.
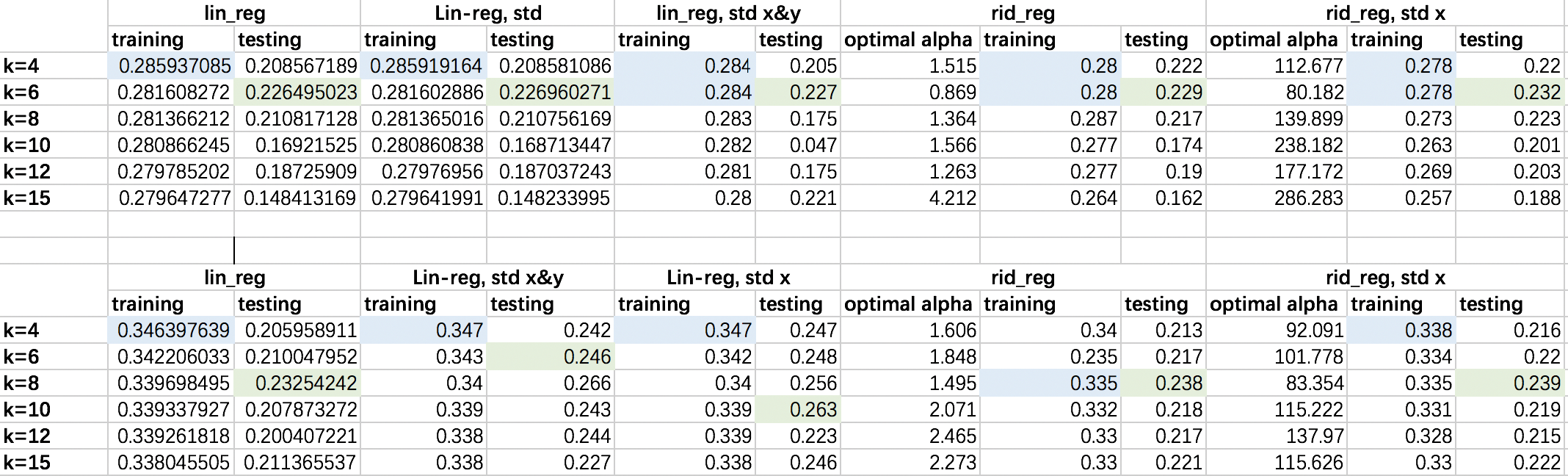
Firstly, for both of these two datasets, there is a general trend that smaller k tends to get a higher training score. That’s probably because (k-1)/k of the dataset is used for training, which means that less data points will be used for training for smaller k. Since there is probably less variation exsiting among less datapoints, the fitted linear model tends to get a higher training score. However, this trend is not too abvious, and as the k gets larger the trainng score does not decrease too much.
We also need to consider testing score to better judge the performance of model. For charles_ask.csv dataset, k=6 always yields the highest testing score. For highter k, such as 10 and above, the training score tends to be much higher than testing score, which indicates overfitting. That’s probably because when data set is split into too many folds, only small amount of dataset are used for testing each time, and any possible variation is exaggerated. When k is low, say k=4, the testing score also tends to be low. That’s probably because the traing data size is not large enough to capture all the information of the whole dataset. For the charles_act.csv dataset we can see highest traing score when k=6,8,10 for different models.
Although the score is still not that approximate to 1, the predictive power has alreay been greatly improved compared to fitting results without zipcode considered. The best among them has training score aroung 0.3 and testing score around 0.25, which could be considered as having moderate predictive power.
Question 6
If we consider both training and testing score, the best model for charles_ask.csv dataset (we will call it model 1)is rid_regression with zipcode included and standardization of features, k=6. The best model for charles_act.csv dataset (we will call it model 2)is linear regression with zipcode included and standardization of both features and targets, k=10. Both of the models could be considered as underfitting. Model 1 only has a tarining score of 0.278 and testing score of 0.232. Model 2 only has a training score of 0.339 and testing score of 0.263. Although they are high enough compared to other models, they are still really not approximate to 1.
From the analysis we can see that including zipcode has significantly improved the predictive power. On the other hand, changing various types/specifications of the model without zipcode included really does not help much with improving scores. This suggests that while we definitely should try different models, getting more information associated with the targets is probably more important.
Given that charleston county is really near to the beach, another information could also be included is the distance from the beach. This might offer a more precise prediction compared to the categorical variable, zipcode. Other information could also be considered include the distance from the Ravenel Waterfront Park/Historic Charleston City Market, or number of restaurants/gyms in the community.